화면 좌표로 gps 좌표 구하는 방법 ($307) · Snippets

음.. 도움이 될지는 모르겠지만, 제 생각을 남겨보겠습니다!

알고 있는 것:

G:gps, S:screen

13m로 표시된 선 끝에 있는 뷰(아이콘이 있는위치?)의 gps 좌표 (G_x1, G_y1) , 화면 좌표 (S_x1, S_y1)
깃발 아이콘이 있는 곳의 gps좌표 (G_x2, G_y2) , 화면 좌표 (S_x2, S_y2)
중앙점의 최초 gps좌표 (G_x0, G_y0) , 화면 좌표 (S_x0, S_y0)
각 좌표 사이의 거리(단위: 미터) -> (위에서 표시된 13m, 111m로 가정)
중앙점을 이동했을 때의 화면 좌표 -> (S_x, S_y)

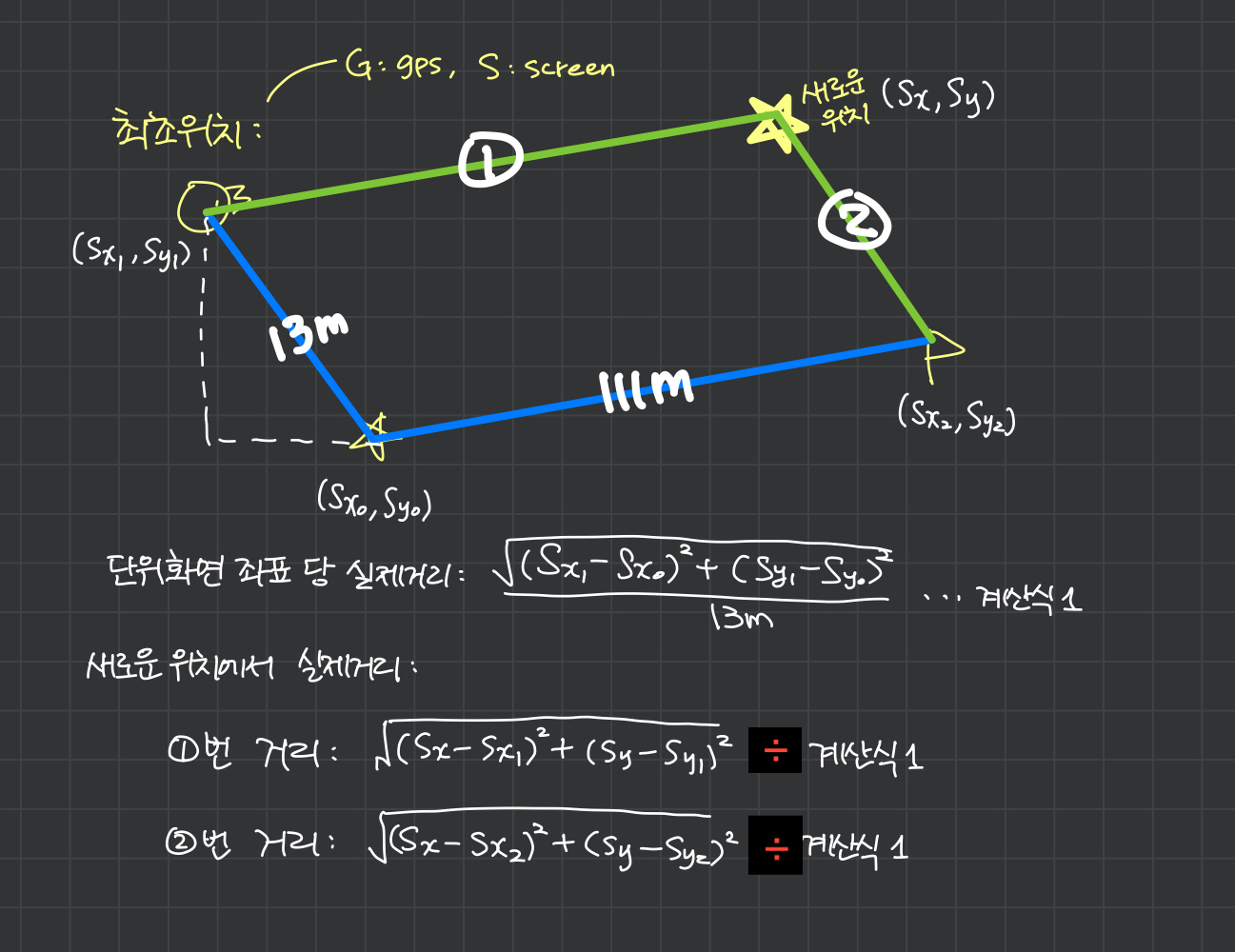
화면좌표를 사용해서 거리 구하기

우선 최초로 데이터를 얻었을 때, 각 좌표 사이의 거리정보와 화면좌표정보를 사용해서 화면좌표와 실제거리를 매칭시킬 수 있습니다.

예) 13m로 표시된 양쪽에서 화면좌표 (S_x1, S_y1) 와 (S_x0, S_y0) 를 피타고라스를 사용하면 화면좌표에서의 거리를 구할 수 있고, 해당 거리에 13m로 나눠주면 화면좌표와 실제거리(m)를 매칭시킬 수 있습니다. (단위 화면좌표 당 실제거리)

계산식1: sqrt((S_x1-S_x0)^2 + (S_y1-S_y0)^2))/13m (단위 화면좌표 당 실제거리)

그 후, 새로운 위치로 이동 했을 때 (S_x, S_y) 이 좌표에서 양쪽에 위치하고 있는 아이콘 (S_x1, S_y1) 와 깃발 (S_x2, S_y2) 에 대해서 피타고라스를 사용하여 화면좌표 상에서의 거리를 구하고 위에서 구했던 단위 화면좌표 당 실제거리를 곱하면 => 실제거리를 업데이트 시킬 수 있다고 생각합니다.

아이콘에서 새로운 위치의 거리: sqrt((S_x-S_x1)^2 + (S_y-S_y1)^2) / (계산식1)
깃발에서 새로운 위치의 거리: sqrt((S_x-S_x2)^2 + (S_y-S_y2)^2) / (계산식1)

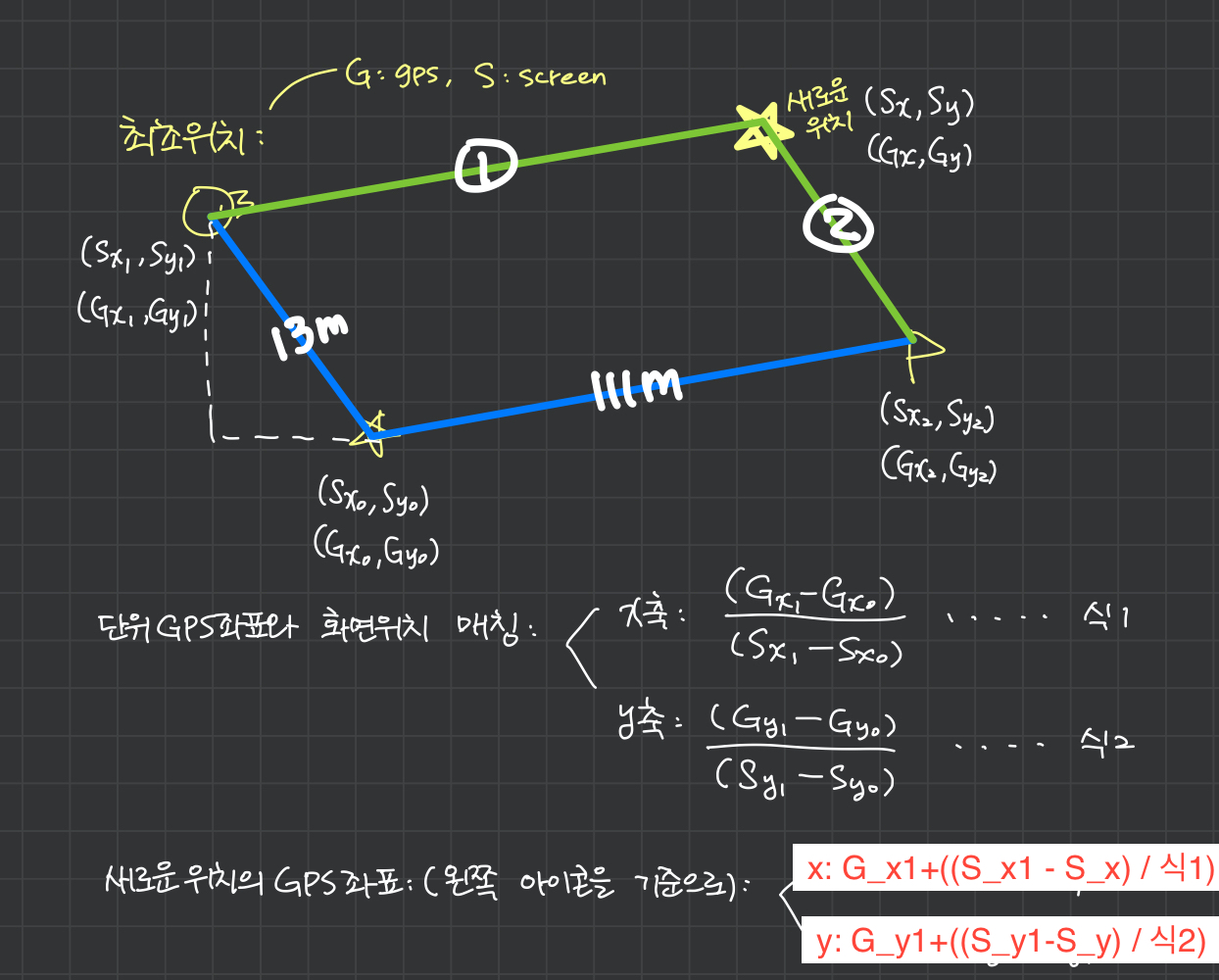
새로 이동된 위치의 GPS좌표 구하기

정확한지는...(지구가 둥글다...)

클릭해서 보기

우선 최초로 데이터를 얻었을 때, 각 좌표 화면위치 정보와 GPS좌표정보를 사용해서 화면위치와 GPS좌표 정보의 대응관계를 구합니다.

예) 13m로 표시된 양쪽에서 화면좌표 (S_x1, S_y1) 와 (S_x0, S_y0) , GPS좌표 (G_x1, G_y1) 와 (G_x0, G_y0) 를 사용해서 단위 GPS좌표 당 화면좌표크기를 구합니다.

x축: (G_x1-G_x0)/(S_x1-S_x0) (단위 GPS좌표(x축) 당 화면좌표크기) --- 식1
y축: (G_y1-G_y0)/(S_y1-S_y0) (단위 GPS좌표(y축) 당 화면좌표크기) --- 식2

그 후, 새로운 위치로 이동 했을 때 (S_x, S_y) 이 좌표에서 양쪽에 위치하고 있는 아이콘 (S_x1, S_y1) 와 깃발 (S_x2, S_y2) 에 대해서 위에서 구한 x축, y축의계산식을 곱하면 => 새로운 위치의 GPS좌표도 구할 수 있습니다.

왼쪽아이콘을 사용해서 계산:
- x: G_x1+((S_x1-S_x)/식1)
- y: G_y1+((S_y1-S_y)/식2)